EDITORIAL | October 3, 2017

[Meta Analysis] Rick and Morty S3E1: The Hacker’s Episode

By Keith Makan

Hi folks, I’m a huge Rick and Morty fan. Sometimes while watching it, I notice allegories and puns related to security, privacy, physics, psychology, and a wide range of scientific fields. Because of this, I’ve decided to review some Rick and Morty episode and share my observations with the wonderful folks who work in these fields and those who aspire to 😉 Enjoy!

A machine force feeding a human. Being brutally and utterly dedicated to our whims, the robots show us how perverted our ideas of success, good, and bad are when taken to an extreme – effectively giving us a taste of our own “medicine.”

Before we dig into what this episode means, here’s a quick summary from Wikipedia:

Rick is interrogated via a mind-computer link inside a galactic federal prison. Rick is interrogated via a mind-computer link inside a galactic federal prison. Summer and Morty attempt to rescue him, but they are captured by SEAL Team Ricks, who take them to the Citadel of Ricks and decide to assassinate Rick. Back at the prison, Rick tricks both the federal agents and his aspiring assassins by switching bodies with them. He then teleports the entire Citadel into the federal prison, prompting a massive battle. Amid the confusion, Rick rescues Morty and Summer and uses the Galactic Federation’s mainframe to make their currency worthless. The Federation falls into chaos and collapses as a result, with the aliens leaving Earth. Back at home, Jerry asks Beth to choose between him and Rick, but she chooses Rick. After the new status quo is established, Rick reveals to Morty that his ulterior motive was to become his de facto male influence. This escalates into a nonsensical angry rant, centered around Rick’s desire to find more of the discontinued McDonald’s Szechuan sauce, a promotional product for the 1998 film Mulan.

– https://en.wikipedia.org/wiki/Rick_and_Morty_(season_3)#Episodes

Lets dig in…

The Brainalyzer

Rick is trapped in something called a “Brainalyzer” which is effectively a brain-to-computer link. This is a computer science pun in a couple of ways. It obviously references cutting-edge computer science research into literally connecting peoples brains to computers. In academic circles, researchers have affected a way to control a computer with your brain or have your brain controlled by a computer.

Rick in the Brainalyzer.

The Brainalyzer also serves as an ironic expression of the false ideology people have of computers: that they are NOT directly connected to our brains.

The software we write for the computer, the hardware we build for the computer, and the perspectives we have of all of these things are entirely inside our heads.

As a hacker, I can tell you that what you do when you try to break someone’s algorithm is basically argue with the person who wrote the algorithm in your head! One person’s implementation of their idea of what security is competes with yours; it’s all mind games. Coming back to the episode, this is literally what Rick is doing in the scene; inside his head, he argues with the person who is ‘securing him’ in the prison.

The flip side of this Brainalyzer – from a security perspective – is that it is a huge security design mistake. Interfacing the thoughts of the prisoners to the prison computer system (which controls the prison) makes separation failure a huge security risk. Ironically, the prison exists to physically restrain the prisoners because they are bad people who think of doing bad things. The Brainalyzer is implemented in utter reverse to this idea; in a sense, it is a way to control the prison in the literal minds of the people they are imprisoning.

Rick’s Mind Virus(es)

The strategy the interrogators employ is to ask Rick to share the memory of his first successful creation of the Portal Gun. Rick then leads them to the memory, which turns out to be a complete fabrication.

Rick’s exploit being uploaded…

What has happened here is Rick has convinced them one kind of information or data in his head is actually another kind of information or data. This is strongly analogous to what is called a memory corruption attack. In a memory corruption attack, the adversary convinces the machine that malicious data (one kind of information) is actually execution code (another kind of data), or that “data” should be treated as literal instructions. This flaw allows the attacker to inject data that is interpreted as code, thereby allowing the attacker’s data to arbitrarily influence the behavior of the machine.

So now we see Rick has triggered a memory corruption bug! And he does this in order to inject code into the machine giving them access to his brain. Rick confirms this by referring to the code he gave them as a “virus,” and stating that he did it to install a backdoor that allows him full control of the facility.

Rick literally psychoanalyzing his opponent – “getting inside his head.”

Rick now has full control of the “memory” they are trapped in and reveals that the entire time he was fooling them. What is ironic about this is that Rick is physically trapped in a machine that allows them direct access to his brain. This is to say while they are “inside his brain,” because Rick was hustling them this whole time, he was actually inside their heads!

Gotta Go Take a Sh*t…

After escaping the Brainalyzer, Rick suddenly needs to use the bathroom on Level 9. This is obviously a social engineering exploit. Restrooms are often located behind security barriers. However, if there is a kind reception person, they can usually be talked into letting you go through to use the bathroom; at which that point, you’ve bypassed security and you’re in! A very old trick, Kevin Mitnick would probably giggle to see Rick haphazardly employ this tactic.

Rick social engineering his way to level 9

The allegory becomes a little more obvious after this scene. Starting from a subtle, nuanced example of a security exploit (by the depth of the metaphor) the plot switches to a more obvious and almost sloppy “gotta go take a sh*t ,” with Rick literally declaring his intention at the end of the episode (speaking in an encapsulating fashion). This “escalation” is a common cadence to security attacks (starting small, ending big): you always start from a small crack and chip away until you have Domain Admin rights. Every hacker knows that!

Just before Rick can make use of the password, he is interrupted by assassins from the council of Ricks. Quickly, he escapes in what is a literal instantiation of an authentication replay or a kind of “session hijacking” attack. Here Rick swaps identities with someone in the group that is trying to catch him, thereby, tricking them into killing the wrong person. Rick has now gone from an interrogator in the prison to a member of SEAL Team Rick. One epic privilege escalation attack!

The Privilege Escalation Attack

After killing the entire SEAL team, he makes his way to the citadel as Rick D99. He then pulls off another obvious privilege escalation attack by specifically asking for someone with a certain level of “higher” clearance.

Rick Phone Phreaking/Hardware Hacking his way into the citadel

Assuming this role, he then moves to gain control of the entire domain and jokes about how bad the system design is (another jab at information security engineering). The design flaw here is that there is no further authentication or oversight needed to perform an incredibly dangerous function; you just walk up to it and press the right buttons – no, executive calls, no approval process…just buttons! He abuses this design as a citadel employee to teleport the entire citadel straight into the galactic prison he just escaped from, causing a massive war between the citadel and the galactic prison.

The person in the center here looks strikingly similar to Rick in the previous image. The armor, the hair. Some might recognize the “Butter Robot”-esque android being built in the background. This is the site banner for DefCon the world’s biggest hacking conference :).

The BitFlip Attack

Following this, Rick makes his way to Level 9, finally admitting his entire scheme was all an elaborate ploy to in fact “get Level 9 access without a password!” He explains his entire chain of exploits as a revenge arch triggered by the citadel interrupting his imminent access to Level 9 by the attempted assassination. Having gained Level 9 access, Rick uses what could be seen as another very old security attack called “Bit Flipping.” This term is sometimes used to loosely refer to attacks that can deterministically change something’s state in a way that affects security. Usually, these “states” are represented using simple Boolean values of 0 or 1. For example, Row Hammer has been exploited to flip bits in a table that holds security relevant information. Effectively, this is what Rick is doing with the currency value: flipping a 1 bit to 0. A small error that eventually topples an entire federation. Start small, end big!

That’s it for now, until I dig up more macabre information security or extra-scientific analogies.

This blog was originally written and posted on September 25, 2017 by Keith Makan and is reproduced here with his express permission.

RESEARCH | July 24, 2015

Differential Cryptanalysis for Dummies

By Keith Makan

Recently, I ventured into the crazy world of differential cryptanalysis purely to find out what the heck it was all about. In this post, I hope to reassure you that this strange and rather cool technique is not as scary as it seems. Hopefully, you’ll be attacking some ciphers of your own in no time!

A differential cryptanalysis attack is a method of abusing pairs of plaintext and corresponding ciphertext to learn about the secret key that encrypted them, or, more precisely, to reduce the amount of time needed to find the key. It’s what is called a chosen plaintext attack; the attacker has access to plaintext and corresponding ciphertext.

We’re going to attack a simple block cipher I stole using another explanation of the technique (links are available at the bottom of the post). This cipher is meant to exhibit a few rudimentary elements of a Substitution-Permutation Network (SPN) (minus some common elements for simplicity), while highlighting the power of the differential technique. So, let’s get started.

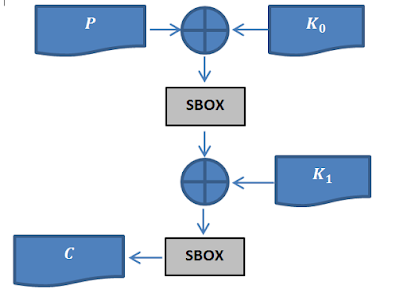
I think a good place to start is to look at the block cipher and check out what makes it tick. Here is a quick schematic of the algorithm:

Where:

C is the cipher-text
K_0, K_1 are the first and second round keys, respectively
P is the plaintext
SBOX is the substitution box.

As you can probably guess from looking at the schematic,: the cipher takes in two 2 sub-keys (K_0,K_1) and a piece of plain-text. It, it then XORs the plain-text with the first key, K_0, then, afterwards pulls the plain-text through a substitution box (SBOX) (we will talk about this little gadget soon). From there, it then takes the output of the SBOX, and XORs it with K_01, and then pulls it through the SBOX again to produce the file piece of final cipher-text. So now that we know how the cipher works, and we can begin formulating our attack.!

To start off with, let’s try writing down this cipher in an algebraic form:

C=SBOX(SBOX(P⨁K_0 )⨁K_1 )

(1)

Great! We can start talking about some of the weird properties of this cipher.

We know that when it comes to the cryptographic security of an encryption function the only thing that should be relied on for Confidentiality is your secret key (these are the words of a great Dutch cryptographer a long time ago [https://en.wikipedia.org/wiki/Auguste_Kerckhoffs]). This means the algorithm, including the workings of the SBOXs, will be known (or rather, in our analysis, we should always assume it will be known) by our attacker. Anything secret in our algorithm cannot be relied on for security. More specifically, any operation that is completely reversible (requiring only knowledge of the ciphertext) is useless!

When it comes to the use of substitution boxes, unless something we don’t know meaningfully obscures the output of the SBOX, using it will not add any security. It will be reduced to a mere reversible “encoding” of its input.

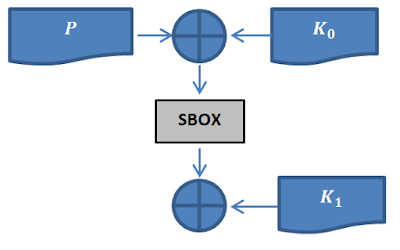
Looking at the algebraic form in (1), we can see the cipher pulls the input through the SBOX again in its last operation before returning it as ciphertext. This operation adds no security at all, especially in the context of a differential attack, because it is trivial to reverse the effect of the last SBOX. To make this clear, imagine knowing the output of the SBOX, but not being capable of knowing the input. Given the context of the last SBOX, this is impossible if you know the ciphertext. We can reduce the encryption function and focus on what actually adds security. The function becomes:

C= SBOX(P⨁K_0 )⨁K_1

(2)

Ironically, the SBOX in this expression (2), is now the only thing that adds security, so it will be the target of our analysis. Consider what would happen if we could know the output of the SBOX, including the plaintext/ciphertext pairs. The entire security of the cipher would fly out the window. After a few XOR operations, we would be able to work out the second key, and by extrapolation, the first key.

But how would we know the SBOX output? Well, what about analyzing the way the SBOX behaves by observing how differences between inputs map to differences in outputs. This insight is at the heart of differential cryptanalysis! Why choose this property? The only thing we have access to is plaintext/ciphertext pairs in a differential cryptanalysis attack (thems the rules), so we need to derive our information from this data. Also, XOR differences have favorable properties under XOR, namely they are unaffected by them. If we look at how the SBOX maps these differences, this is what we get:

∆x	∆y	count	[(x,x^’), (y,y^’)]
15	4	1	[(0, 15), (3, 7)]
15	7	1	[(3, 12), (10, 13)]
15	6	2	[(4, 11), (4, 2)] [(5, 10), (9, 15)]
5	15	1	[(3, 6), (10, 5)]
5	10	2	[(0, 5), (3, 9)] [(1, 4), (14, 4)]
3	15	1	[(1, 2), (14, 1)]
3	12	2	[(5, 6), (9, 5)] [(13, 14), (12, 0)]
3	10	2	[(8, 11), (8, 2)] [(12, 15), (13, 7)]
5	2	1	[(11, 14), (2, 0)]
5	4	1	[(8, 13), (8, 12)]
5	7	1	[(2, 7), (1, 6)]
5	6	1	[(9, 12), (11, 13)]
5	8	1	[(10, 15), (15, 7)]
4	15	1	[(10, 14), (15, 0)]
4	12	1	[(3, 7), (10, 6)]
1	7	1	[(14, 15), (0, 7)]
1	1	1	[(12, 13), (13, 12)]

Where

∆x = x⊕x^’
∆y = y⊕y^’
x^’,x is the input pair to the SBOX
y’,y is the output pair of from the SBOX
And ∆x→ ∆y is a differential characteristic
Count is the number of times the differential characteristic appears

This table is a small sample of the data collected from the SBOX.

This mapping of the XOR difference in the input to the XOR difference in the output is called a differential characteristic. Hence the name, “differential” cryptanalysis.! We can now use this data to steal the secret key.! Given the cipher-text/plain-text pairs, we need to find one encrypted under our target key that satisfies one of the differential characteristics. To find that pair you need to do the following:

Consider a sample differential characteristic a →b (this can be any differential):

Choose (or generate) one plain-text P, and produce another plain-text P^’=P⨁a , where a is an input differential (notice that the XOR difference of P and P’ is a!)
Encrypt the two plain-texts (P,P’) to get (C,C’)
If C⨁C’ = b, then you have a good pair!

If you know that a →b is the differential that suits your text pair, you now know what the potential input/output pairs are for the SBOX, because of thanks to the analysis we did earlier on. ! So now given these pairs, you can try different calculations for the key. You will likely have a couple possible keys, but one of them will definitely be the correct one.

For example, let’s say we have the following setup:

The keys K_0, K_1 : 0,6

(p,p’) :=> (c,c’) : input_diff :=> output_diff : [count, [(sI,sI’),(sO,sO’)]… ]

(3,12) -> (11, 12) : 15 :=> 7 : [1, [[(3, 12), (10, 13)]]]

(5,10) -> (9, 15) : 15 :=> 6 : [2, [[(4, 11), (4, 2)], [(5, 10), (9, 15)]]]

(4,11) -> (4, 2) : 15 :=> 6 : [2, [[(4, 11), (4, 2)], [(5, 10), (9, 15)]]]

(5,10) -> (9, 15) : 15 :=> 6 : [2, [[(4, 11), (4, 2)], [(5, 10), (9, 15)]]]

(3,6) -> (3, 12) : 5 :=> 15 : [1, [[(3, 6), (10, 5)]]]

The script that generated this output is available at the end of the post.

We need to select a plain-text/cipher-text pair and use the information associated to with them the pair to calculate the key. So for example let’s use, using (3,12) => (11,12), we can then calculate the K_0, K_1 in the following way:

Given then that (from the last operation of the cipher):

C=K_1⊕ S_o

We know that (because of how XOR works):

K_1=C⊕ S_o

Although we have a couple of choices for those values, so we need to run through them.

Given that:

K_0,K_1=(11,12)

C=(11,12) this is a tuple because we are using a pair of cipher-texts

P=(3,12)

S_i=(3,12)

S_o=(10,13)

We can then try to calculate the second round key as:

K_1=C[0]⊕ S_o [0]=1 wrong!

K_1=C[0]⊕ S_o [1]=6 right!

(3)

We can also calculate K_0, namely:

K_0=P[1]⊕ S_i [0]= wrong!

K_0=C[0]⊕ S_o [1]= wrong!

K_0=C[0]⊕ S_o [0]=0 right!

(4)

We’ve just derived the two sub keys.! Cryptanalysis successful!

The weird behavior of the SBOX under differential mapping is what makes differential cryptanalysis possible, but it this is not to say that this is the ONLY way to perform differential cryptanalysis. The property we are using here (XOR differences) is merely one application of this concept. You should think about differential cryptanalysis as leveraging any operation in an encryption function that can be used to “explain” differences in input/output pairs. So when you’re done reading about this application, look at some of the other common operations in encryption functions and think about what else, besides SBOXs, can be abused in this way; what other properties of the input/outputs pairs have interesting behaviors under common operations?.

Also, it may be useful to think about how you can extend this application of differential cryptanalysis in order to attack multi-round ciphers (i.e. ciphers that are built using multiple rounds of computation of ciphers like the one we’ve attacked here).