Recently, I ventured into the crazy world of differential cryptanalysis purely to find out what the heck it was all about. In this post, I hope to reassure you that this strange and rather cool technique is not as scary as it seems. Hopefully, you’ll be attacking some ciphers of your own in no time!

A differential cryptanalysis attack is a method of abusing pairs of plaintext and corresponding ciphertext to learn about the secret key that encrypted them, or, more precisely, to reduce the amount of time needed to find the key. It’s what is called a chosen plaintext attack; the attacker has access to plaintext and corresponding ciphertext.

We’re going to attack a simple block cipher I stole using another explanation of the technique (links are available at the bottom of the post). This cipher is meant to exhibit a few rudimentary elements of a Substitution-Permutation Network (SPN) (minus some common elements for simplicity), while highlighting the power of the differential technique. So, let’s get started.

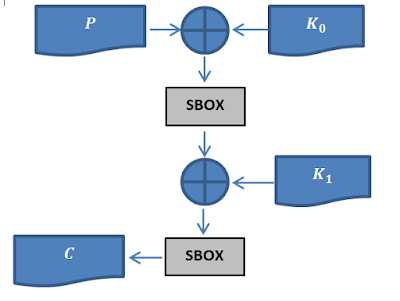
I think a good place to start is to look at the block cipher and check out what makes it tick. Here is a quick schematic of the algorithm:

Where:

As you can probably guess from looking at the schematic,: the cipher takes in two 2 sub-keys (K_0,K_1) and a piece of plain-text. It, it then XORs the plain-text with the first key, K_0, then, afterwards pulls the plain-text through a substitution box (SBOX) (we will talk about this little gadget soon). From there, it then takes the output of the SBOX, and XORs it with K_01,  and then pulls it through the SBOX again to produce the file piece of final cipher-text. So now that we know how the cipher works, and we can begin formulating our attack.!

To start off with, let’s try writing down this cipher in an algebraic form: 

C=SBOX(SBOX(P⨁K_0 )⨁K_1 )

(1)

Great! We can start talking about some of the weird properties of this cipher.

We know that when it comes to the cryptographic security of an encryption function the only thing that should be relied on for Confidentiality is your secret key (these are the words of a great Dutch cryptographer a long time ago [https://en.wikipedia.org/wiki/Auguste_Kerckhoffs]). This means the algorithm, including the workings of the SBOXs, will be known (or rather, in our analysis, we should always assume it will be known) by our attacker. Anything secret in our algorithm cannot be relied on for security. More specifically, any operation that is completely reversible (requiring only knowledge of the ciphertext) is useless!

When it comes to the use of substitution boxes, unless something we don’t know meaningfully obscures the output of the SBOX, using it will not add any security. It will be reduced to a mere reversible “encoding” of its input.

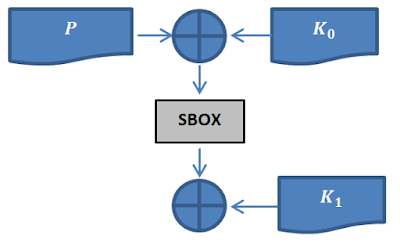
Looking at the algebraic form in (1), we can see the cipher pulls the input through the SBOX again in its last operation before returning it as ciphertext. This operation adds no security at all, especially in the context of a differential attack, because it is trivial to reverse the effect of the last SBOX. To make this clear, imagine knowing the output of the SBOX, but not being capable of knowing the input. Given the context of the last SBOX, this is impossible if you know the ciphertext. We can reduce the encryption function and focus on what actually adds security. The function becomes:

C= SBOX(P⨁K_0 )⨁K_1

(2)

Ironically, the SBOX in this expression (2), is now the only thing that adds security, so it will be the target of our analysis. Consider what would happen if we could know the output of the SBOX, including the plaintext/ciphertext pairs. The entire security of the cipher would fly out the window. After a few XOR operations, we would be able to work out the second key, and by extrapolation, the first key.

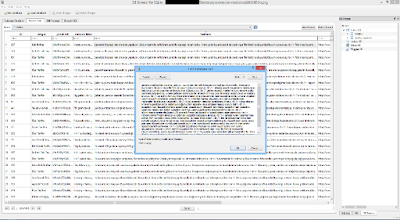
But how would we know the SBOX output? Well, what about analyzing the way the SBOX behaves by observing how differences between inputs map to differences in outputs. This insight is at the heart of differential cryptanalysis! Why choose this property? The only thing we have access to is plaintext/ciphertext pairs in a differential cryptanalysis attack (thems the rules), so we need to derive our information from this data. Also, XOR differences have favorable properties under XOR, namely they are unaffected by them. If we look at how the SBOX maps these differences, this is what we get:

∆x	∆y	count	[(x,x^’), (y,y^’)]
15	4	1	[(0, 15), (3, 7)]
15	7	1	[(3, 12), (10, 13)]
15	6	2	[(4, 11), (4, 2)] [(5, 10), (9, 15)]
5	15	1	[(3, 6), (10, 5)]
5	10	2	[(0, 5), (3, 9)] [(1, 4), (14, 4)]
3	15	1	[(1, 2), (14, 1)]
3	12	2	[(5, 6), (9, 5)] [(13, 14), (12, 0)]
3	10	2	[(8, 11), (8, 2)] [(12, 15), (13, 7)]
5	2	1	[(11, 14), (2, 0)]
5	4	1	[(8, 13), (8, 12)]
5	7	1	[(2, 7), (1, 6)]
5	6	1	[(9, 12), (11, 13)]
5	8	1	[(10, 15), (15, 7)]
4	15	1	[(10, 14), (15, 0)]
4	12	1	[(3, 7), (10, 6)]
1	7	1	[(14, 15), (0, 7)]
1	1	1	[(12, 13), (13, 12)]

Where

This table is a small sample of the data collected from the SBOX.

This mapping of the XOR difference in the input to the XOR difference in the output is called a differential characteristic. Hence the name, “differential” cryptanalysis.! We can now use this data to steal the secret key.! Given the cipher-text/plain-text pairs, we need to find one encrypted under our target key that satisfies one of the differential characteristics. To find that pair you need to do the following:

Consider a sample differential characteristic a →b (this can be any differential):

For example, let’s say we have the following setup:

The keys K_0, K_1 : 0,6

 (p,p’) :=> (c,c’) : input_diff :=> output_diff : [count, [(sI,sI’),(sO,sO’)]… ]

 (3,12) -> (11, 12) : 15 :=> 7 : [1, [[(3, 12), (10, 13)]]]

 (5,10) -> (9, 15) : 15 :=> 6 : [2, [[(4, 11), (4, 2)], [(5, 10), (9, 15)]]]

 (4,11) -> (4, 2) : 15 :=> 6 : [2, [[(4, 11), (4, 2)], [(5, 10), (9, 15)]]]

 (5,10) -> (9, 15) : 15 :=> 6 : [2, [[(4, 11), (4, 2)], [(5, 10), (9, 15)]]]

 (3,6) -> (3, 12) : 5 :=> 15 : [1, [[(3, 6), (10, 5)]]]

The script that generated this output is available at the end of the post.

We need to select a plain-text/cipher-text pair and use the information associated to with them the pair to calculate the key.  So for example let’s use, using (3,12) => (11,12), we can then calculate the K_0, K_1 in the following way:

Given then that (from the last operation of the cipher):

C=K_1⊕ S_o

We know that (because of how XOR works):

K_1=C⊕ S_o

Although we have a couple of choices for those values, so we need to run through them.

Given that:

K_0,K_1=(11,12)

C=(11,12) this is a tuple because we are using a pair of cipher-texts

P=(3,12)

S_i=(3,12)

S_o=(10,13)

We can then try to calculate the second round key as:

K_1=C[0]⊕ S_o [0]=1   wrong!

K_1=C[0]⊕ S_o [1]=6   right!

(3)

We can also calculate K_0, namely:

K_0=P[1]⊕ S_i [0]=   wrong!

K_0=C[0]⊕ S_o [1]=   wrong!

K_0=C[0]⊕ S_o [0]=0    right!

(4)

We’ve just derived the two sub keys.! Cryptanalysis successful!

The weird behavior of the SBOX under differential mapping is what makes differential cryptanalysis possible, but it this is not to say that this is the ONLY way to perform differential cryptanalysis. The property we are using here (XOR differences) is merely one application of this concept. You should think about differential cryptanalysis as leveraging any operation in an encryption function that can be used to “explain” differences in input/output pairs. So when you’re done reading about this application, look at some of the other common operations in encryption functions and think about what else, besides SBOXs, can be abused in this way; what other properties of the input/outputs pairs have interesting behaviors under common operations?.

Also, it may be useful to think about how you can extend this application of differential cryptanalysis in order to attack multi-round ciphers (i.e. ciphers that are built using multiple rounds of computation of ciphers like the one we’ve attacked here).

Further Reading and References:

Some Scripts to play around with: