Entropy
“In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits. In this context, a ‘message’ means a specific realization of the random variable.” [1]
1. http://en.wikipedia.org/wiki/Entropy_%28information_theory%29
I find myself analyzing password and token entropy quite frequently and I’ve come to rely upon Wolfram Alpha and Burp Suite Pro to get my estimates for these values. It’s understandable why we’d want to check a password’s entropy. It gives us an indication of how long it would take an attacker to brute force it, whether in a login form or a stolen database of hashes. However, an overlooked concern is the entropy contained in tokens for session and object identifiers. These values can also be brute forced to steal active sessions and gain access to objects to which we do not have permission. Not only are these tokens sometimes too short, they sometimes also contain much less entropy than appears.
Estimating Password Entropy
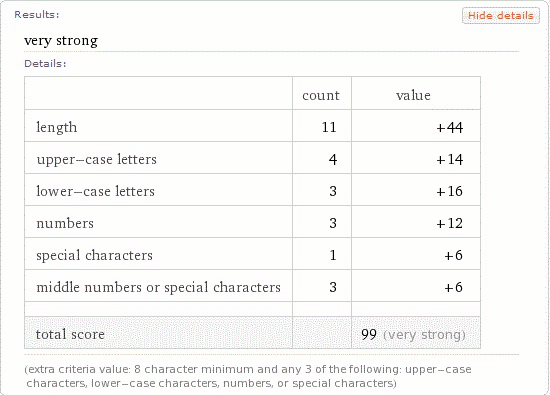
Wolfram Alpha has a keyword specifically for analyzing passwords.
http://www.wolframalpha.com/input/?i=password+strength+f00b4r^LYFE
Estimating Token Entropy
Estimating the solution for: [ characters ^ length = 2 ^ x ] will convert an arbitrary string value to bits of entropy. This formula is not really solvable, so I use Wolfram Alpha to estimate the solution.
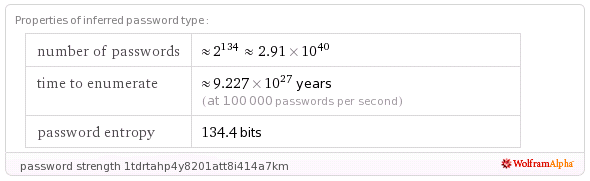
e.g. 1tdrtahp4y8201att8i414a7km has the formula:
http://www.wolframalpha.com/input/?i=36^26+%3D+2^x
Click “Approximate Form” under the “Real solution”:
The password strength calculator also works okay on tokens, and we’ll see a similar result:
http://www.wolframalpha.com/input/?i=password+strength+1tdrtahp4y8201att8i414a7km
BUT! Analysis of a single token is not enough to measure /effective/ entropy. Burp Suite Sequencer will run the proper entropy analysis tests on batches of session identifiers to estimate this value. Send your application login request (or whatever request generates a new token value) to the Sequencer and configure the Sequencer to collect the target token value. Start collecting and set the “Auto-Analyze” box to watch as Burp runs its tests.
A sample token “1tdrtahp4y8201att8i414a7km” from this application has an estimated entropy of 134.4 bits, but FIPS analysis of a batch of 2000 of these identifiers shows an effective entropy of less than 45 bits!
Not only that, but the tokens range in length from 21 to 26 characters, some are much shorter than we originally thought.
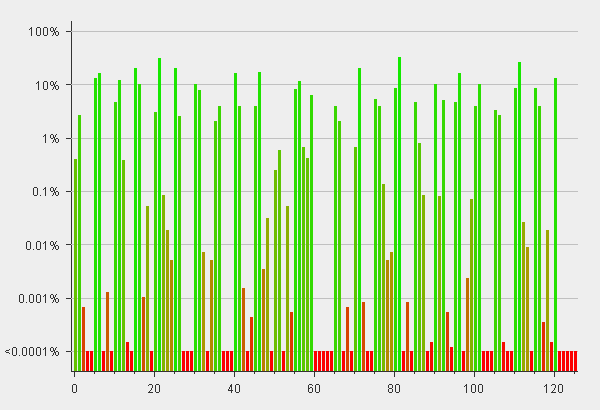
Burp will show you many charts, but these bit-level analysis charts will give you an idea of where the tokens are failing to meet expected entropy.
You can spot a highly non-random value near the middle of the token (higher is better), and the varying length of the tokens drag down entropy near the end. The ASCII-based character set used in the token have one or more unused or underused bits, as seen in the interspersed areas of very low entropy.
In the case illustrated above I would ask the client to change the way randomness is supplied to the token and/or increase the token complexity with a hashing function, which should increase attack resistance.
Remember, for session or object identifiers, you want to get close to 128 bits of /effective/ entropy to prevent brute forcing. This is a guideline set by OWASP and is in line with most modern web application frameworks.
If objects persist for long periods or are very numerous (in the millions) you’ll want more entropy to maintain the same level of safety as a session identifier, which is more ephemeral. An example of persistent objects (on the order of years) which rely on high entropy tokens would be Facebook photo URLs. Photos marked private are still publicly accessible, but Facebook counts on the fact that their photo URLs have high entropy.
The following URL has at least 160 bits of entropy:
https://fbcdn-sphotos-a.akamaihd.net/hphotos-ak-ash4/398297_10140657048323225_750784224_11609676_1712639207_n.jpg
For passwords, the analysis is a little more subjective, but Wolfram Alpha gives you a good estimate. You can use this password analysis for encryption keys or passphrases as well, e.g. if they are provided as part of a source code audit.
Happy Hacking!